A Recent Survey Concluded That The Proportion Of American - We are given the sample proportion, which is p ^ = 0.27. We are also given the true population proportion, which is p = 0.29. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. The true population proportion of american. The true population proportion of american teenagers who have a cell phone is 0.29. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. The true population proportion of american. For samples of size 1,000 that are selected at. The true population proportion of american. A recent survey concluded that the proportion of american teenager who have a cell phone is 0.27.
For samples of size 1,000 that are selected at. The true population proportion of american. The true population proportion of american. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. To solve this question, we need to find the mean and standard deviation for the sampling distribution of the sample proportion of. A recent survey concluded that the proportion of american teenager who have a cell phone is 0.27. The true population proportion of american. Study with quizlet and memorize flashcards containing terms like if you choose an srs of size n from a population with a given p1 and. The true population proportion of american teenagers who have a cell phone is 0.29. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27.
A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. The true population proportion of american teenagers who have a cell phone is 0.29. The true population proportion of american. A recent survey concluded that the proportion of american teenager who have a cell phone is 0.27. We are given the sample proportion, which is p ^ = 0.27. The true population proportion of american. To solve this question, we need to find the mean and standard deviation for the sampling distribution of the sample proportion of. Study with quizlet and memorize flashcards containing terms like if you choose an srs of size n from a population with a given p1 and. We are also given the true population proportion, which is p = 0.29. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27.
What Percentage Of Americans Are Black 2024 Gert Guenevere
A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. A recent survey concluded that the proportion of american teenager who have a cell phone is 0.27. Study with quizlet and memorize flashcards containing terms like.
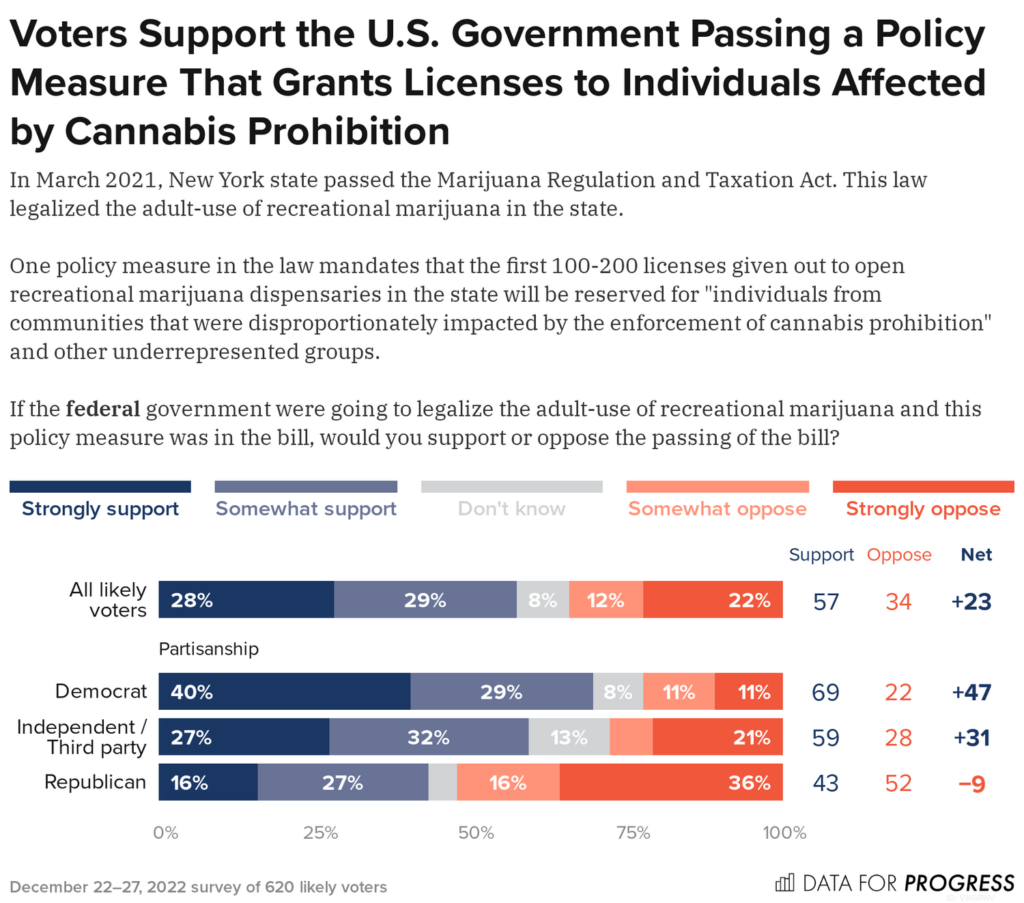
Majority Of American Voters—Including Most Republicans—Back Federal
A recent survey concluded that the proportion of american teenager who have a cell phone is 0.27. The true population proportion of american. For samples of size 1,000 that are selected at. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. We are given the sample proportion, which is p ^ =.
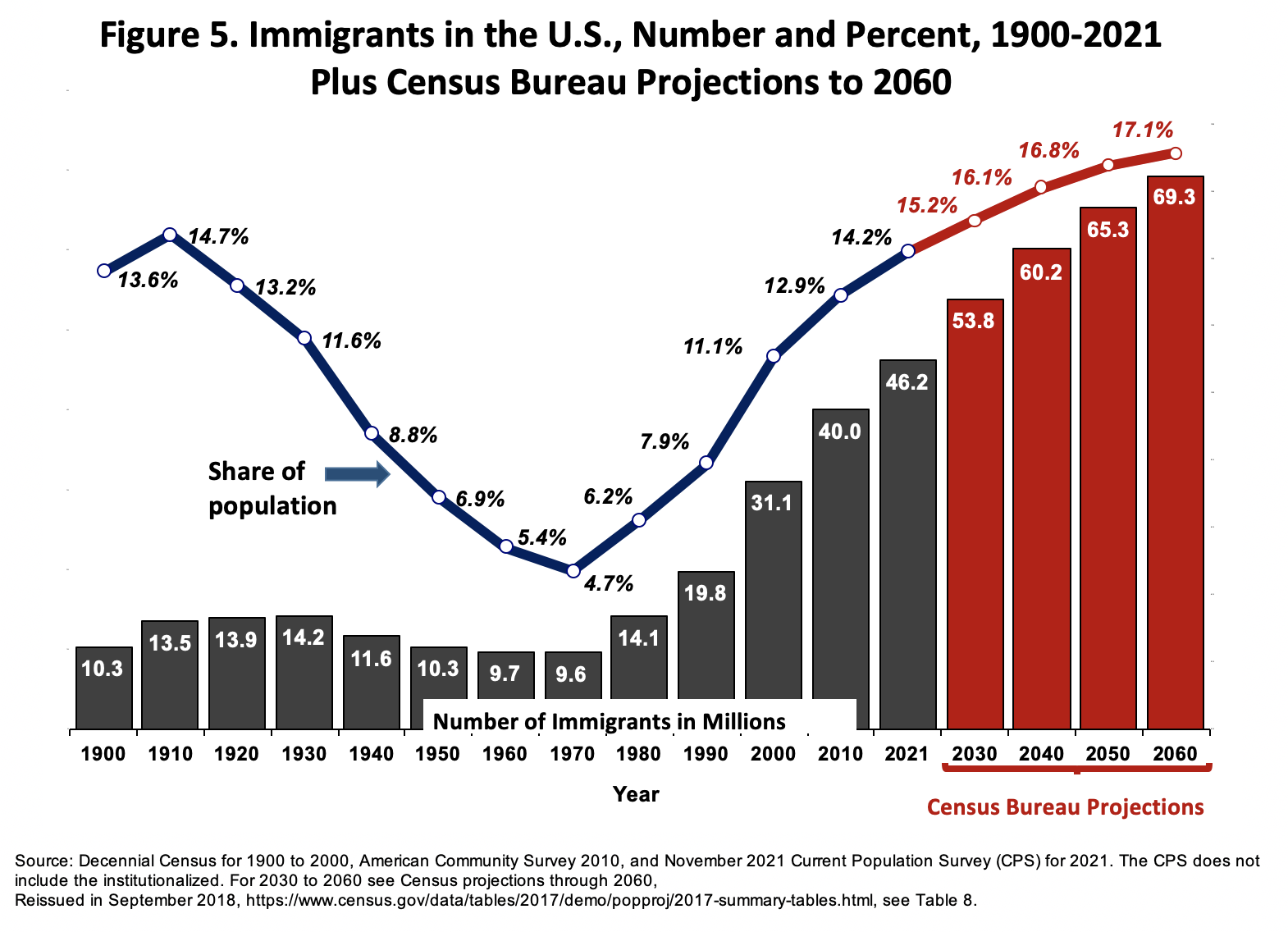
Immigrant Population Hits Record 46.2 Million in Nov 2021
A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. We are also given the true population proportion, which is p = 0.29. For samples of size 1,000 that are selected at. The true population proportion.
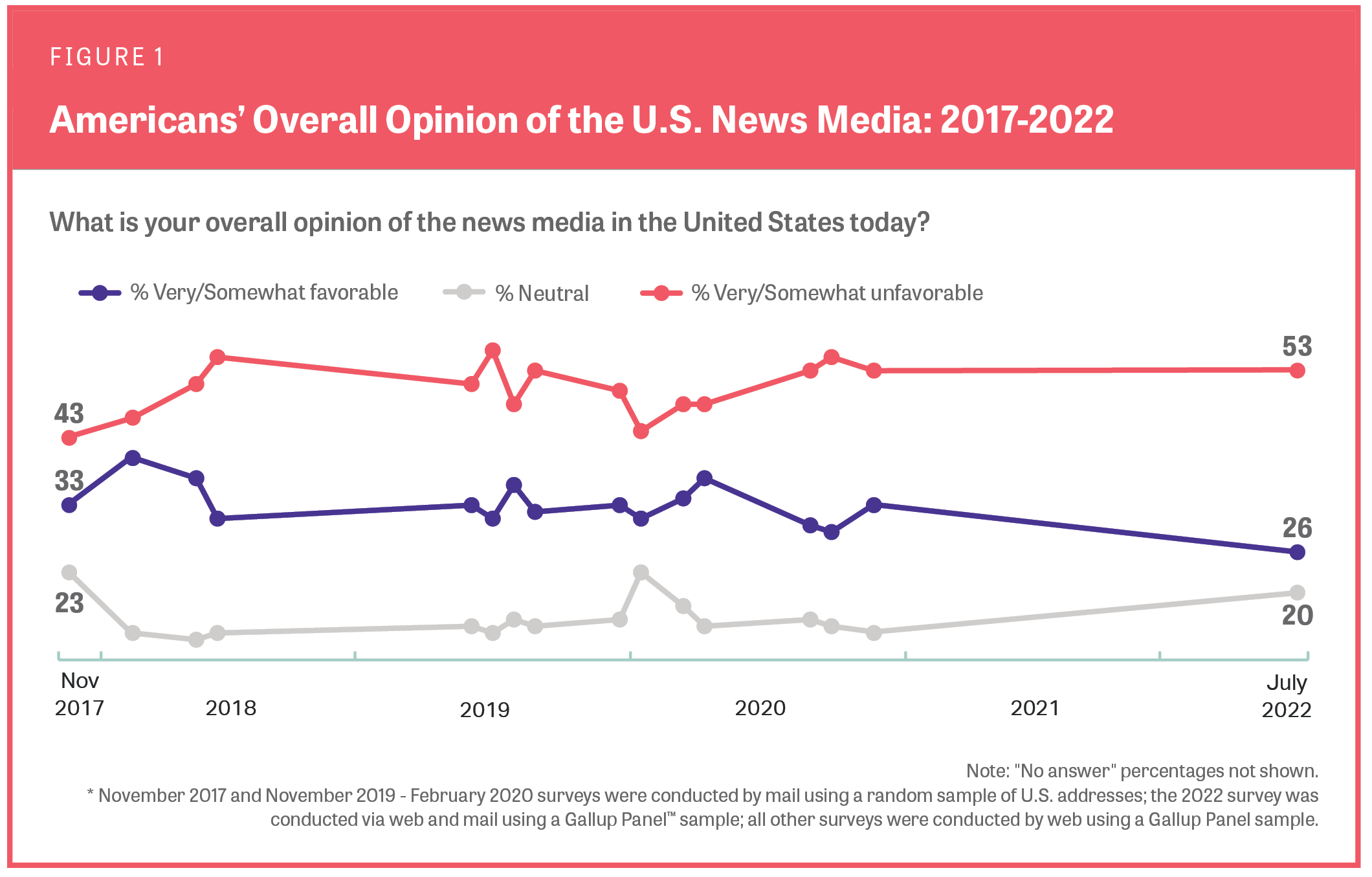
American Views 2022 Part 2, Trust Media and Democracy Knight Foundation
The true population proportion of american teenagers who have a cell phone is 0.29. The true population proportion of american. To solve this question, we need to find the mean and standard deviation for the sampling distribution of the sample proportion of. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. The.
SOLVED A national survey of 1,000 adults was conducted on May 13,2013
A recent survey concluded that the proportion of american teenager who have a cell phone is 0.27. We are also given the true population proportion, which is p = 0.29. The true population proportion of american teenagers who have a cell phone is 0.29. For samples of size 1,000 that are selected at. A recent survey concluded that the proportion.
Proportion of survey participants compared with university reported
For samples of size 1,000 that are selected at. We are also given the true population proportion, which is p = 0.29. A recent survey concluded that the proportion of american teenager who have a cell phone is 0.27. The true population proportion of american. The true population proportion of american.
Proportion of Survey Respondents From Across the Country (N = 128
The true population proportion of american teenagers who have a cell phone is 0.29. For samples of size 1,000 that are selected at. To solve this question, we need to find the mean and standard deviation for the sampling distribution of the sample proportion of. A recent survey concluded that the proportion of american teenager who have a cell phone.
SOLVED Time magazine reported the result of a telephone poll of 605
A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. For samples of size 1,000 that are selected at. Study with quizlet and memorize flashcards containing terms like if you choose an srs of size n from a population with a given p1 and. We are given the sample proportion, which is p.
1. Proportion of nationwide survey respondents residing in the nine
The true population proportion of american teenagers who have a cell phone is 0.29. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. Study with quizlet and memorize flashcards containing terms like if you choose an srs of size n from a population with a given p1 and. To solve this question,.
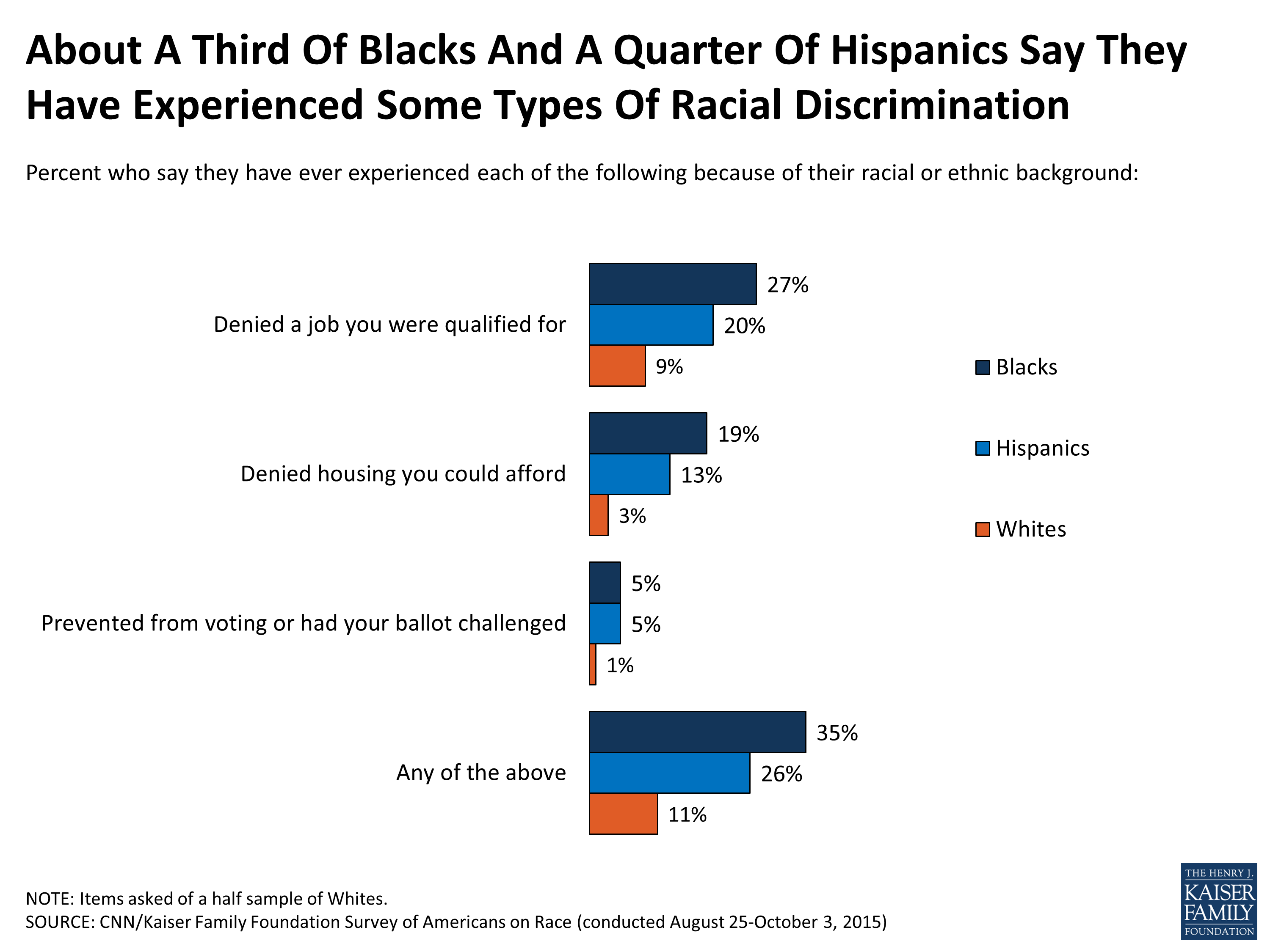
Survey of Americans on Race, Section 1 Racial Discrimination, Bias
We are also given the true population proportion, which is p = 0.29. We are given the sample proportion, which is p ^ = 0.27. For samples of size 1,000 that are selected at. Study with quizlet and memorize flashcards containing terms like if you choose an srs of size n from a population with a given p1 and. The.
A Recent Survey Concluded That The Proportion Of American Teenager Who Have A Cell Phone Is 0.27.
Study with quizlet and memorize flashcards containing terms like if you choose an srs of size n from a population with a given p1 and. We are given the sample proportion, which is p ^ = 0.27. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27. We are also given the true population proportion, which is p = 0.29.
The True Population Proportion Of American Teenagers Who Have A Cell Phone Is 0.29.
For samples of size 1,000 that are selected at. The true population proportion of american. To solve this question, we need to find the mean and standard deviation for the sampling distribution of the sample proportion of. A recent survey concluded that the proportion of american teenagers who have a cell phone is 0.27.
The True Population Proportion Of American.
The true population proportion of american.