Riemann Sheets - Intuitively, a riemann surface is just an object which looks like c when you. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. Di erent choice for z is the square root with positive imaginary part. This is uniquely de ned away from the positive real axis, and. To start, we begin by giving some examples of riemann surfaces.
Intuitively, a riemann surface is just an object which looks like c when you. Di erent choice for z is the square root with positive imaginary part. To start, we begin by giving some examples of riemann surfaces. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. This is uniquely de ned away from the positive real axis, and.
To start, we begin by giving some examples of riemann surfaces. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. This is uniquely de ned away from the positive real axis, and. Di erent choice for z is the square root with positive imaginary part. Intuitively, a riemann surface is just an object which looks like c when you.
Partition of the complex kplane and choices of the Riemann sheets for
This is uniquely de ned away from the positive real axis, and. Di erent choice for z is the square root with positive imaginary part. Intuitively, a riemann surface is just an object which looks like c when you. To start, we begin by giving some examples of riemann surfaces. Functions of one complex variable spring 2003 notes on riemann.
(a) Four Riemann sheets of the multivalued function D({k}_{{\rm{z
This is uniquely de ned away from the positive real axis, and. To start, we begin by giving some examples of riemann surfaces. Di erent choice for z is the square root with positive imaginary part. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. Intuitively, a riemann surface.
(a) Four Riemann sheets of the multivalued function D({k}_{{\rm{z
To start, we begin by giving some examples of riemann surfaces. Di erent choice for z is the square root with positive imaginary part. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. Intuitively, a riemann surface is just an object which looks like c when you. This is.
Relevant regions of twochannel Riemann sheets. The red ray, with two
To start, we begin by giving some examples of riemann surfaces. Intuitively, a riemann surface is just an object which looks like c when you. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. Di erent choice for z is the square root with positive imaginary part. This is.
The complex w plane and the two kplane Riemann sheets with branch cuts
Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. Di erent choice for z is the square root with positive imaginary part. To start, we begin by giving some examples of riemann surfaces. Intuitively, a riemann surface is just an object which looks like c when you. This is.
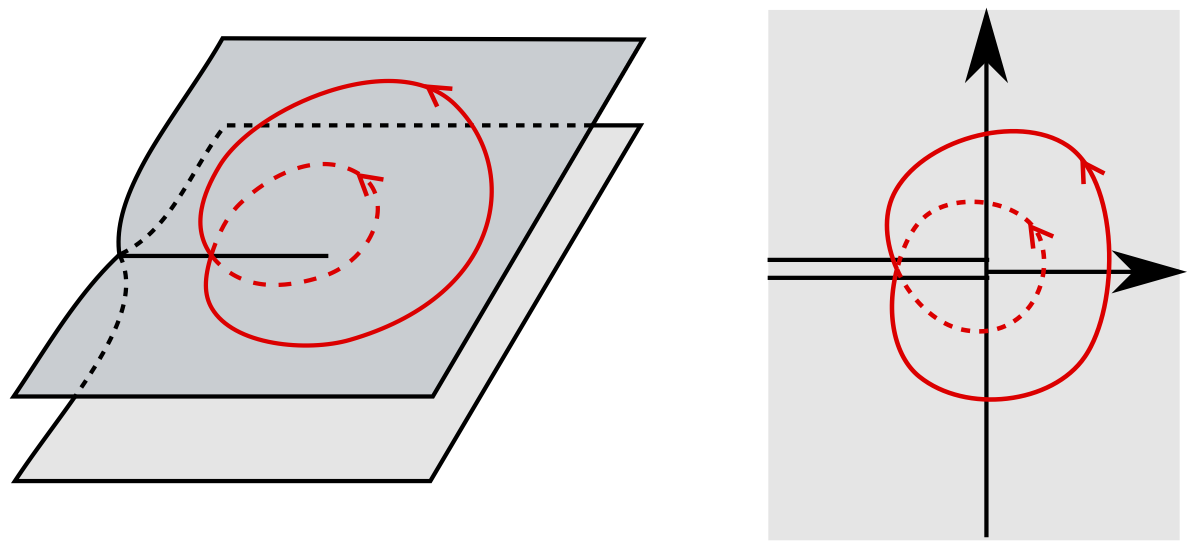
Sketch of the Riemann surface of the multivalued function f (z) = √ z
This is uniquely de ned away from the positive real axis, and. To start, we begin by giving some examples of riemann surfaces. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. Intuitively, a riemann surface is just an object which looks like c when you. Di erent choice.
Tracking RayleighBloch waves swapping between Riemann sheets
To start, we begin by giving some examples of riemann surfaces. Intuitively, a riemann surface is just an object which looks like c when you. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. This is uniquely de ned away from the positive real axis, and. Di erent choice.
(a) Four Riemann sheets of the multivalued function D({k}_{{\rm{z
This is uniquely de ned away from the positive real axis, and. Intuitively, a riemann surface is just an object which looks like c when you. Di erent choice for z is the square root with positive imaginary part. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. To.
Topological Galois Theory
Di erent choice for z is the square root with positive imaginary part. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. Intuitively, a riemann surface is just an object which looks like c when you. This is uniquely de ned away from the positive real axis, and. To.
The pole locations and residues given by our fits. The Riemann sheets
Intuitively, a riemann surface is just an object which looks like c when you. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. To start, we begin by giving some examples of riemann surfaces. Di erent choice for z is the square root with positive imaginary part. This is.
Intuitively, A Riemann Surface Is Just An Object Which Looks Like C When You.
Di erent choice for z is the square root with positive imaginary part. Functions of one complex variable spring 2003 notes on riemann surfaces riemann surfaces are a special case of a more. This is uniquely de ned away from the positive real axis, and. To start, we begin by giving some examples of riemann surfaces.